Baby Shark Dance
On November 2, 2020, Baby Shark Dance surpassed Despacito to become the most-watched YouTube video of all time, with more than 7 billion views.
Suppose that YouTube itself is implemented in C.
- (1 point.) In no more than three sentences, what problem might YouTube run into if using an
intto store each video’s number of views?
One solution to that problem is to use “arbitrary-precision integers” that can represent integers of any size. In C, for instance, we could use a linked list to implement arbitrary-precision integers by defining a new type as follows:
typedef struct node
{
int digit;
struct node *next;
}
node;
In this representation, each (decimal) digit of an integer is stored in a node in a linked list. Each node stores the digit itself (digit), 0 through 9, and a pointer to the next digit (next), which is NULL if there is no next digit. The digits themselves are stored in reverse order (i.e., from least-significant digit to most-significant digit). For example, 123 would be represented in memory as:
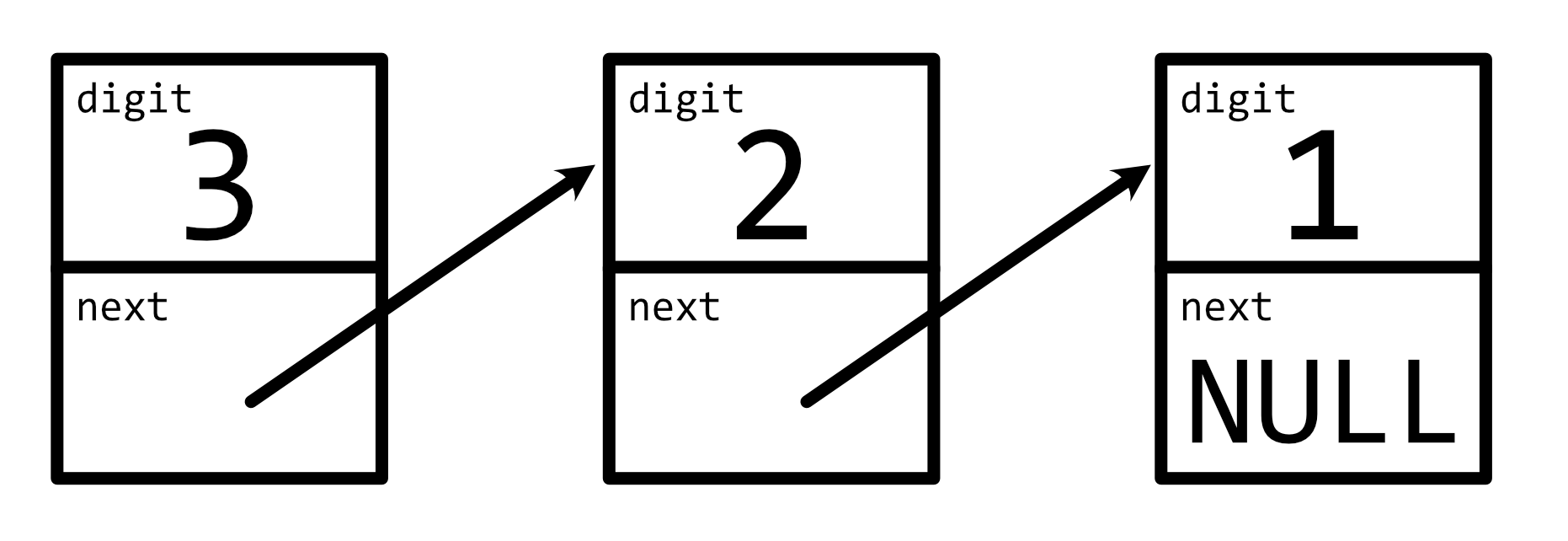
Even though you couldn’t print an integer in this representation using printf alone, you could with a (recursive) function like:
void print(node *n)
{
if (n != NULL)
{
print(n->next);
printf("%i", n->digit);
}
}
-
(2 points.) Are there integers that can be represented using this representation that cannot be represented using an
intalone? Provide an example or explain in no more than three sentences why no such example exists. -
(2 points.) Are there integers that can be represented using an
intalone that cannot be represented using this representation (assuming no changes to it)? Provide an example or explain in no more than three sentences why no such example exists.
Consider shark/integers.c, below, wherein each of n, a, and b is a pointer to the first node in a linked list:
#include <stdbool.h>
#include <stdlib.h>
typedef struct node
{
int digit;
struct node *next;
}
node;
bool divisible_by_three(node *n)
{
// TODO
}
bool equal(node *a, node *b)
{
// TODO
}
void increment(node *n)
{
// TODO
}
-
(3 points.) In
shark/integers.c, complete the implementation ofdivisible_by_threein such a way that the function returnstrueif the integer represented bynis divisible by 3 orfalseif it is not. A number is divisible by 3 if and only if the sum of its digits is also divisible by 3. Assume that the sum will fit in anint. And assume thatnwill not beNULL. Do not alter the definition ofnodeor the return types or parameters of any functions. And do not add additional functions tointegers.c. -
(3 points.) In
shark/integers.c, complete the implementation ofequalin such a way that the function returnstrueif the integers represented byaandbare equal (even if their pointers are different) orfalseif they are not. Assume that neitheranorbwill beNULL. And assume that neitheranorbwill have zeroes at the ends of their linked lists (which would otherwise be “leading zeroes”). Do not alter the definition ofnodeor the return types or parameters of any functions. And do not add additional functions tointegers.c. -
(6 points.) In
shark/integers.c, complete the implementation ofincrementin such a way that it adds 1 to the integer represented byn. For example, ifninitially represents50, thennshould ultimately represent51. Assume thatmallocwill not returnNULL. Assume thatnwill not beNULL. Do not alter the definition ofnodeor the return types or parameters of any functions. And do not add additional functions tointegers.c.
You might find shark/testing.c of some help!