Quiz 2

Quizzes are optional, but encouraged. They are a good way to test your conceptual understanding, before diving into the programming projects. Consider each question below, then reveal the answer. If you didn’t get it right, consider why you may have had that misunderstanding!

Question 1

Consider a standard 52-card deck of cards with 13 card values (Ace, King, Queen, Jack, and 2-10) in each of the four suits (clubs, diamonds, hearts, spades). If a card is drawn at random, what is the probability that it is a spade or a two?

Note that “or” in this question refers to inclusive, not exclusive, or.

• About 0.019
• About 0.077
• About 0.17
• About 0.25
• About 0.308
• About 0.327
• About 0.5
• None of the above

Question 2

Imagine flipping two fair coins, where each coin has a Heads side and a Tails side, with Heads coming up 50% of the time and Tails coming up 50% of the time. What is probability that after flipping those two coins, one of them lands heads and the other lands tails?

Question 3

Recall the Bayesian Network shown in lecture, reproduced below.

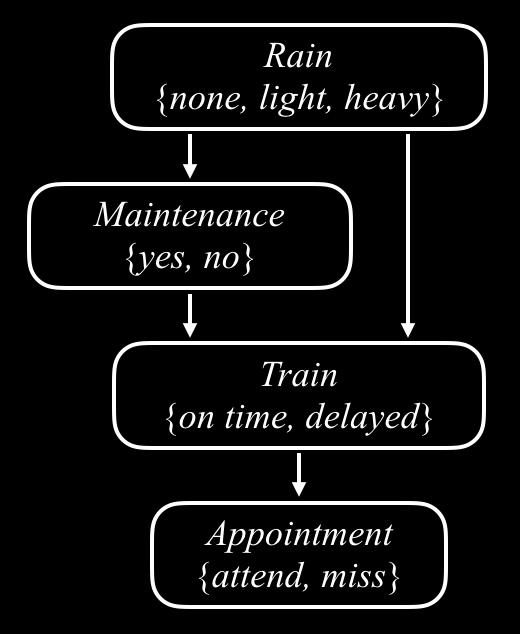
Which of the following sentences is true?

• Assuming we know the train is on time, whether or not there is rain affects the probability that the appointment is attended.
• Assuming we know there is rain, whether or not there is track maintenance does not affect the probability that the train is on time.
• Assuming we know there is track maintenance, whether or not there is rain does not affect the probability that the train is on time.
• Assuming we know the train is on time, whether or not there is track maintenance does not affect the probability that the appointment is attended.
• Assuming we know there is track maintenance, whether or not there is rain does not affect the probability that the appointment is attended.

Question 4

Two factories — Factory A and Factory B — design batteries to be used in mobile phones. Factory A produces 60% of all batteries, and Factory B produces the other 40%. 2% of Factory A’s batteries have defects, and 4% of Factory B’s batteries have defects. What is the probability that a battery is both made by Factory A and defective?

• 0.008
• 0.012
• 0.02
• 0.024
• 0.028
• 0.06
• 0.12
• 0.2
• 0.429
• 0.6
• None of the above