Lecture 3
- Welcome!
- Linear Search
- Binary Search
- Running Time
- search.c
- Data Structures
- Sorting
- Bubble Sort
- Recursion
- Merge Sort
- Summing Up
Welcome!
- In week zero, we introduced the idea of an algorithm: a black box that may take an input and creates an output.
- This week, we are going to expand upon our understanding of algorithms through pseudocode and into code itself.
- Also, we are going to consider the efficiency of these algorithms. Indeed, we are going to be building upon our understanding of how to use some of the lower-level concepts we discussed last week in building algorithms.
-
Recall back to earlier in the course when we introduced the following graph:
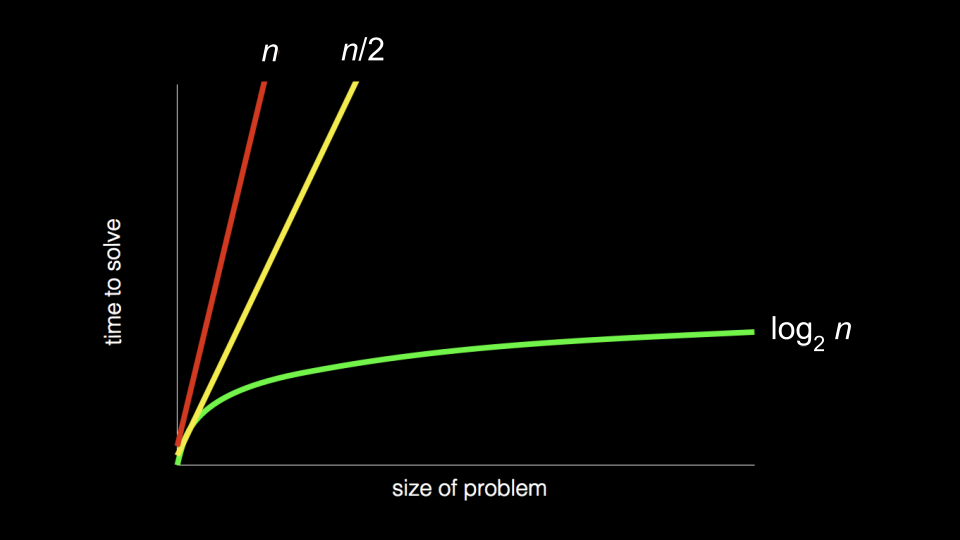
- As we step into this week, you should consider how the way an algorithm works with a problem may determine the time it takes to solve a problem! Algorithms can be designed to be more and more efficient, to a limit.
- Today, we will focus upon the design of algorithms and how to measure their efficiency.
Linear Search
- Recall that last week you were introduced to the idea of an array, blocks of memory that are consecutive: side-by-side with one another.
-
You can metaphorically imagine an array like a series of seven red lockers as follows:
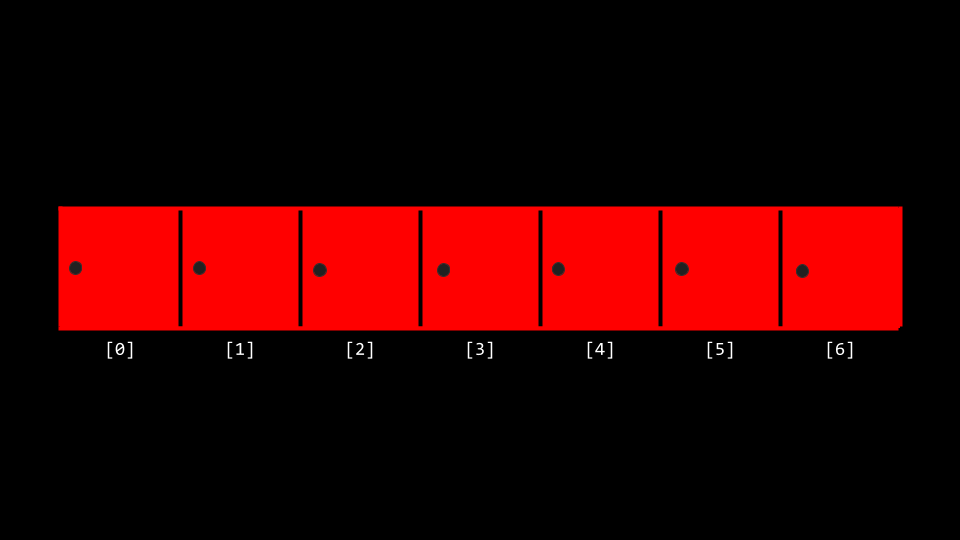
- We can imagine that we have an essential problem of wanting to know, “Is the number 50 inside an array?” A computer must look at each locker to be able to see if the number 50 is inside. We call this process of finding such a number, character, string, or other item searching.
-
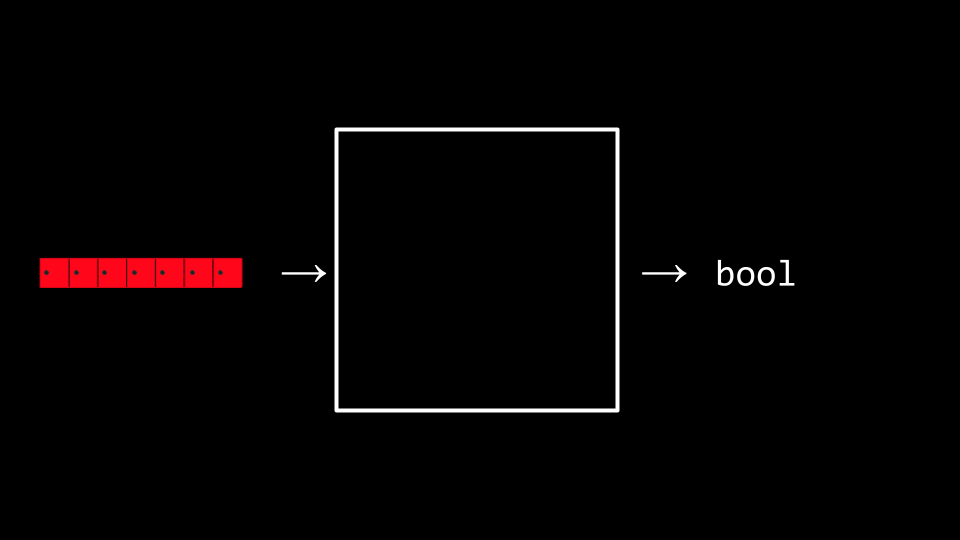
We can potentially hand our array to an algorithm, wherein our algorithm will search through our lockers to see if the number 50 is behind one of the doors: Returning the value true or false.
-
We can imagine various instructions we might provide our algorithm to undertake this task as follows:
For each door from left to right If 50 is behind door Return true Return falseNotice that the above instructions are called pseudocode: A human-readable version of the instructions that we could provide the computer.
-
A computer scientist could translate that pseudocode as follows:
For i from 0 to n-1 If 50 is behind doors[i] Return true Return falseNotice that the above is still not code, but it is a pretty close approximation of what the final code might look like.
Binary Search
- Binary search is another search algorithm that could be employed in our task of finding the 50.
-
Assuming that the values within the lockers have been arranged from smallest to largest, the pseudocode for binary search would appear as follows:
If no doors left Return false If 50 is behind middle door Return true Else if 50 < middle door Search left half Else if 50 > middle door Search right half -
Using the nomenclature of code, we can further modify our algorithm as follows:
If no doors left Return false If 50 is behind doors[middle] Return true Else if 50 < doors[middle] Search doors[0] through doors[middle - 1] Else if 50 > doors[middle] Search doors[middle + 1] through doors[n - 1]Notice, looking at this approximation of code, you can nearly imagine what this might look like in actual code.
Running Time
-
running time involves an analysis using big O notation. Take a look at the following graph:
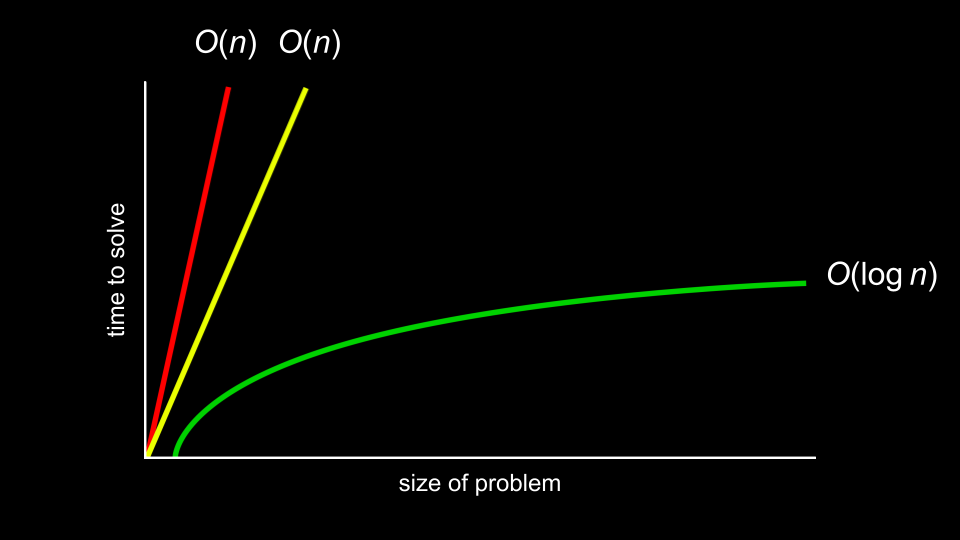
- Rather than being ultra-specific about the mathematical efficiency of an algorithm, computer scientists discuss efficiency in terms of the order of various running times.
- In the above graph, the first algorithm is \(O(n)\) or in the order of n. The second is in \(O(n)\) as well. The third is in \(O(\log n)\).
-
It’s the shape of the curve that shows the efficiency of an algorithm. Some common running times we may see are:
- \(O(n^2)\)
- \(O(n \log n)\)
- \(O(n)\)
- \(O(\log n)\)
- \(O(1)\)
- Of the running times above, \(O(n^2)\) is considered the worst running time, \(O(1)\) is the fastest.
- Linear search was of order \(O(n)\) because it could take n steps in the worst case to run.
- Binary search was of order \(O(\log n)\) because it would take fewer and fewer steps to run even in the worst case.
- Programmers are interested in both the worst case, or upper bound, and the best case, or lower bound.
- The \(\Omega\) symbol is used to denote the best case of an algorithm, such as \(\Omega(\log n)\).
- The \(\Theta\) symbol is used to denote where the upper bound and lower bound are the same, where the best case and the worst case running times are the same.
- As you continue to develop your knowledge in computer science, you will explore these topics in more detail in future courses.
search.c
-
You can implement linear search ourselves by typing
code search.cin your terminal window and by writing code as follows:#include <cs50.h> #include <stdio.h> int main(void) { // An array of integers int numbers[] = {20, 500, 10, 5, 100, 1, 50}; // Search for number int n = get_int("Number: "); for (int i = 0; i < 7; i++) { if (numbers[i] == n) { printf("Found\n"); return 0; } } printf("Not found\n"); return 1; }Notice that the line beginning with
int numbers[]allows us to define the values of each element of the array as we create it. Then, in theforloop, we have an implementation of linear search.return 0is used to indicate success and exit the program.return 1is used to exist the program with an error (failure). - We have now implemented linear search ourselves in C!
-
What if we wanted to search for a string within an array? Modify your code as follows:
#include <cs50.h> #include <stdio.h> #include <string.h> int main(void) { // An array of strings string strings[] = {"battleship", "boot", "cannon", "iron", "thimble", "top hat"}; // Search for string string s = get_string("String: "); for (int i = 0; i < 6; i++) { if (strcmp(strings[i], s) == 0) { printf("Found\n"); return 0; } } printf("Not found\n"); return 1; }Notice that we cannot utilize
==as in our previous iteration of this program. Instead, we usestrcmp, which comes from thestring.hlibrary.strcmpwill return0if the strings are the same. -
Indeed, running this code allows us to iterate over this array of strings to see if a certain string was within it. However, if you see a segmentation fault, where a part of memory was touched by your program that it should not have access to, do make sure you have
i < 6noted above instead ofi < 7. -
We can combine these ideas of both numbers and strings into a single program. Type
code phonebook.cinto your terminal window and write code as follows:#include <cs50.h> #include <stdio.h> #include <string.h> int main(void) { // Arrays of strings string names[] = {"Carter", "David", "John"}; string numbers[] = {"+1-617-495-1000", "+1-617-495-1000", "+1-949-468-2750"}; // Search for name string name = get_string("Name: "); for (int i = 0; i < 3; i++) { if (strcmp(names[i], name) == 0) { printf("Found %s\n", numbers[i]); return 0; } } printf("Not found\n"); return 1; }Notice that Carter’s number begins with
+1-617, David’s phone number starts with+1-617, and John’s number starts with+1-949. Therefore,names[0]is Carter andnumbers[0]is Carter’s number. This code will allow us to search the phonebook to for a person’s specific number. - While this code works, there are numerous inefficiencies. Indeed, there is a chance that people’s names and numbers may not correspond. Wouldn’t be nice if we could create our own data type where we could associate a person with the phone number?
Data Structures
- It turns out that C allows a way by which we can create our own data types via a
struct. - Would it not be useful to create our own data type called a
person, that has inside of it anameandnumber. -
Modify your code as follows:
#include <cs50.h> #include <stdio.h> #include <string.h> typedef struct { string name; string number; } person; int main(void) { person people[3]; people[0].name = "Carter"; people[0].number = "+1-617-495-1000"; people[1].name = "David"; people[1].number = "+1-617-495-1000"; people[2].name = "John"; people[2].number = "+1-949-468-2750"; // Search for name string name = get_string("Name: "); for (int i = 0; i < 3; i++) { if (strcmp(people[i].name, name) == 0) { printf("Found %s\n", people[i].number); return 0; } } printf("Not found\n"); return 1; }Notice that the code begins with
typedef structwhere a new datatype calledpersonis defined. Inside apersonis a string callednameand astringcalled number. In themainfunction, begin by creating an array calledpeoplethat is of typepersonthat is a size of 3. Then, we update the names and phone numbers of the two people in ourpeoplearray. Most important, notice how the dot notation such aspeople[0].nameallows us to access thepersonat the 0th location and assign that individual a name.
Sorting
- Sorting is the act of taking an unsorted list of values and transforming this list into a sorted one.
- When a list is sorted, searching that list is far less taxing on the computer. Recall that we can use binary search on a sorted list, but not on an unsorted one.
- It turns out that there are many different types of sorting algorithms.
- Selection sort is one such search algorithm.
-
We can represent an array as follows:
-
The algorithm for selection sort in pseudocode is:
For i from 0 to n–1 Find smallest number between numbers[i] and numbers[n-1] Swap smallest number with numbers[i] -
Summarizing those steps, the first time iterating through the list took
n - 1steps. The second time, it tookn - 2steps. Carrying this logic forward, the steps required could be represented as follows:(n - 1) + (n - 2) + (n - 3) + ... + 1 - This could be simplified to n(n-1)/2 or, more simply, \(O(n^2)\).
Bubble Sort
- Bubble sort is another sorting algorithm that works by repeatedly swapping elements to “bubble” larger elements to the end.
-
The pseudocode for bubble sort is:
Repeat n-1 times For i from 0 to n–2 If numbers[i] and numbers[i+1] out of order Swap them If no swaps Quit - As we further sort the array, we know more and more of it becomes sorted, so we only need to look at the pairs of numbers that haven’t been sorted yet.
-
Analyzing selection sort, we made only seven comparisons. Representing this mathematically, where n represents the number of cases, it could be said that selection sort can be analyzed as:
(n - 1) + (n - 2) + (n - 3) + ... + 1or, more simply \(n^2/2 - n/2\).
- Considering that mathematical analysis, n2 is really the most influential factor in determining the efficiency of this algorithm. Therefore, selection sort is considered to be of the order of \(O(n^2)\) in the worst case where all values are unsorted. Even when all values are sorted, it will take the same number of steps. Therefore, the best case can be noted as \(\Omega(n^2)\). Since both the upper bound and lower bound cases are the same, the efficiency of this algorithm as a whole can be regarded as \(\Theta(n^2)\).
- Analyzing bubble sort, the worst case is \(O(n^2)\). The best case is \(\Omega(n)\).
- You can visualize a comparison of these algorithms.
Recursion
- How could we improve our efficiency in our sorting?
-
Recursion is a concept within programming where a function calls itself. We saw this earlier when we saw…
If no doors left Return false If number behind middle door Return true Else if number < middle door Search left half Else if number > middle door Search right halfNotice that we are calling
searchon smaller and smaller iterations of this problem. -
Similarly, in our pseudocode for Week 0, you can see where recursion was implemented:
1 Pick up phone book 2 Open to middle of phone book 3 Look at page 4 If person is on page 5 Call person 6 Else if person is earlier in book 7 Open to middle of left half of book 8 Go back to line 3 9 Else if person is later in book 10 Open to middle of right half of book 11 Go back to line 3 12 Else 13 Quit -
This code could have been simplified, to highlight its recursive properties as follows:
1 Pick up phone book 2 Open to middle of phone book 3 Look at page 4 If person is on page 5 Call person 6 Else if person is earlier in book 7 Search left half of book 9 Else if person is later in book 10 Search right half of book 12 Else 13 Quit -
Consider how in Week 1 we wanted to create a pyramid structure as follows:
# ## ### #### -
To implement this using recursion, type
code recursion.cinto your terminal window and write code as follows:#include <cs50.h> #include <stdio.h> void draw(int n); int main(void) { draw(1); } void draw(int n) { for (int i = 0; i < n; i++) { printf("#"); } printf("\n"); draw(n + 1); }Notice that the draw function calls itself. Further, note that your code may get caught in an infinite loop. To break from this loop, if you get stuck, hit
ctrl-con your keyboard. The reason this creates an infinite loop is that there is nothing telling the program to end. There is no case where the program is done. -
We can correct our code as follows:
#include <cs50.h> #include <stdio.h> void draw(int n); int main(void) { // Get height of pyramid int height = get_int("Height: "); // Draw pyramid draw(height); } void draw(int n) { // If nothing to draw if (n <= 0) { return; } // Draw pyramid of height n - 1 draw(n - 1); // Draw one more row of width n for (int i = 0; i < n; i++) { printf("#"); } printf("\n"); }Notice the base case will ensure the code does not run forever. The line
if (n <= 0)terminates the recursion because the problem has been solved. Every timedrawcalls itself, it calls itself byn-1. At some point,n-1will equal0, resulting in thedrawfunction returning and the program will end.
Merge Sort
- We can now leverage recursion in our quest for a more efficient sort algorithm and implement what is called merge sort, a very efficient sort algorithm.
-
The pseudocode for merge sort is quite short:
If only one number Quit Else Sort left half of number Sort right half of number Merge sorted halves -
Consider the following list of numbers:
6341 -
First, merge sort asks, “is this one number?” The answer is “no,” so the algorithm continues.
6341 -
Second, merge sort will now split the numbers down the middle (or as close as it can get) and sort the left half of numbers.
63|41 -
Third, merge sort would look at these numbers on the left and ask, “is this one number?” Since the answer is no, it would then split the numbers on the left down the middle.
6|3 -
Fourth, merge sort will again ask , “is this one number?” The answer is yes this time! Therefore, it will quit this task and return to the last task it was running at this point:
63|41 -
Fifth, merge sort will sort the numbers on the left.
36|41 -
Now, we return to where we left off in the pseudocode now that the left side has been sorted. A similar process of steps 3-5 will occur with the right-hand numbers. This will result in:
36|14 -
Both halves are now sorted. Finally, the algorithm will merge both sides. It will look at the first number on the left and the first number on the right. It will put the smaller number first, then the second smallest. The algorithm will repeat this for all numbers, resulting in:
1346 - Merge sort is complete, and the program quits.
- Merge sort is a very efficient sort algorithm with a worst case of \(O(n \log n)\). The best case is still \(\Omega(n \log n)\) because the algorithm still must visit each place in the list. Therefore, merge sort is also \(\Theta(n \log n)\) since the best case and worst case are the same.
- A final visualization was shared.
Summing Up
In this lesson, you learned about algorithmic thinking and building your own data types. Specifically, you learned…
- Algorithms.
- Big O notation.
- Binary search and linear search.
- Various sort algorithms, including bubble sort, selection sort, and merge sort.
- Recursion.
See you next time!